.png)
Hirarki Chomsky
AutomataAutomata adalah mesin abstrak yang dapat mengenali (recognize), menerima (accept), atau membangkitkan (generate) sebuah kalimat dalam bahasa tertentu.
Beberapa Pengertian Dasar :
• Simbol adalah sebuah entitas abstrak (seperti halnya pengertian titik dalam geometri). Sebuah huruf atau sebuah angka adalah contoh simbol.
• String adalah deretan terbatas (finite) simbol-simbol. Sebagai contoh, jika a, b, dan c adalah tiga buah simbol maka abcb adalah sebuah string yang dibangun dari ketiga simbol tersebut.
• Jika w adalah sebuah string maka panjang string dinyatakan sebagai |w| dan didefinisikan sebagai cacahan (banyaknya) simbol yang menyusun string tersebut. Sebagai contoh, jika w = abcb maka |w|= 4.
• String hampa adalah sebuah string dengan nol buah simbol. String hampa dinyatakan dengan simbol ε (atau ^) sehingga |ε|= 0. String hampa dapat dipandang sebagai simbol hampa karena keduanya tersusun dari nol buah simbol.
• Alfabet adalah hinpunan hingga (finite set) simbol-simbol.
Grammar dan Klasifikasi ChomskyGrammar G didefinisikan sebagai pasangan 4 tuple : VT, VN, S, Q dan dituliskan sebagai G(VT ,VN ,S , Q), dimana:
VT : himpunan simbol-simbol terminal (atau himpunan token -token, atau alfabet).
VN : himpunan simbol-simbol non terminal.
S ∈ VN : simbol awal (atau simbol start).
Q : himpunan produksi.
Berdasarkan komposisi bentuk ruas kiri dan ruas kanan produksinya (α → β), Noam Chomsky mengklasifikasikan 4 tipe grammar :VN : himpunan simbol-simbol non terminal.
S ∈ VN : simbol awal (atau simbol start).
Q : himpunan produksi.
1. Grammar tipe ke-0 : Unrestricted Grammar (UG)
. Ciri : α, β ∈ (VT | VN) *, α> 0
2. Grammar tipe ke-1 : Context Sensitive Grammar (CSG)
. Ciri : α, β ∈ (VT | VN) *, 0 < α ≤ β
3. Grammar tipe ke-2 : Context Free Grammar (CFG)
. Ciri : α ∈ VN, β ∈ (VT | VN) *
. Ciri : α, β ∈ (VT | VN) *, α> 0
2. Grammar tipe ke-1 : Context Sensitive Grammar (CSG)
. Ciri : α, β ∈ (VT | VN) *, 0 < α ≤ β
3. Grammar tipe ke-2 : Context Free Grammar (CFG)
. Ciri : α ∈ VN, β ∈ (VT | VN) *
4. Grammar tipe ke-3 : Regular Grammar (RG)
. Ciri : α ∈ VN, β ∈ { VT , VT VN} atau α ∈ VN, β ∈ { VT , VN VT}
.. Ciri : α ∈ VN, β ∈ { VT , VT VN} atau α ∈ VN, β ∈ { VT , VN VT}
Automata Hingga (AH)
AH didefinisikan sebagai pasangan 5 tupel : (Q, V T , σ, q0, F):
• Q : himpunan hingga stata
• VT : himpunan hingga simbol input (alfabet)
• σ : fungsi transisi, menggambarkan transisi stata AH akibat pembacaan simbol input.
Fungsi transisi ini biasanya diberikan dalam bentuk tabel.• VT : himpunan hingga simbol input (alfabet)
• σ : fungsi transisi, menggambarkan transisi stata AH akibat pembacaan simbol input.
• q0 ∈ Q : stata awal
• F ⊂ Q : himpunan stata penerima
Ada dua jenis automata hingga : deterministik (AHD, DFA = deterministic finite automata) dan non deterministik (AHN, NFA = non deterministik finite automata).• F ⊂ Q : himpunan stata penerima
- AHD : transisi stata AH akibat pembacaan sebuah simbol bersifat tertentu.
. σ (AHD) : Q × V T → Q
- AHN : transisi stata AH akibat pembacaan sebuah simbol bersifat tak tentu.
. σ (AHN) : Q × V T → 2Q
Automata Hingga Deterministik (AHD). σ (AHD) : Q × V T → Q
- AHN : transisi stata AH akibat pembacaan sebuah simbol bersifat tak tentu.
. σ (AHN) : Q × V T → 2Q
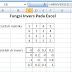
Berikut ini sebuah contoh AHD F(Q, V T , σ, q0, Z), dimana :
Q = {q0, q1, q2} σ diberikan dalam tabel berikut :
Gambar1. Tabel AHD
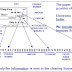
Ilustrasi graf untuk AHD F adalah sebagai berikut :Lambang stata awal adalah node dengan anak panah.
Lambang stata awal adalah node ganda.
Gambar 2. Grafik AHD
Contoh kalimat yang tidak diterima AHD : bb, abb, abba
AHD ini menerima semua kalimat yang tersusun dari simbol a dan b yang tidak mengandung substring bb. sebuah kalimat diterima oleh AHD jika tracingnya berakhir di salah satu stata penerima.
.
Automata Hingga Nondeterministik (AHN)
Berikut ini sebuah contoh AHN F(Q, V T , σ, q0, Z), dimana :
Q = {q 0 , q1, q 2 ,q 3 , q 4 } σ diberikan dalam tabel berikut :
Gambar3. Tabel AHN
Gambar4. Grafik AHN
Contoh kalimat yang diterima AHN di atas : aa, bb, cc, aaa, abb, bcc, cbbContoh kalimat yang tidak diterima AHN di atas : a, b, c, ab, ba, ac, bc
Fungsi transisi σ sebuah AHN dapat diperluas sebagai berikut :
1. σ (q, ε) = {q} untuk setiap q ∈ Q
2. σ (q, t T) = ∪ σ (p i , T) dimana t ∈ V T , T adalah V T *, dan σ (q, t) = {p i }
3. σ ({q1, q2, …, qn}, x) = ∪ σ (q i ,x), untuk x ∈ V T *
Sebuah kalimat di terima AHN jika salah satu tracing-nya berakhir di stata penerima, atau himpunan stata setelah membaca string tersebut mengandung stata penerima.2. σ (q, t T) = ∪ σ (p i , T) dimana t ∈ V T , T adalah V T *, dan σ (q, t) = {p i }
3. σ ({q1, q2, …, qn}, x) = ∪ σ (q i ,x), untuk x ∈ V T *
.
Ekuivalensi AHN, AHD, dan GR
AHD bisa dibentuk dari AHN.GR bisa dibentuk dari AHD. AHN
AHN bisa dibentuk dari GR. AHD GR
Pembentukan AHD dari AHN:
Diberikan sebuah AHN F = (Q, V T , σ, q0, Z). Akan dibentuk sebuah AHD F’ = (Q’, VT ’, σ’, q0’, Z’) dari AHN F tersebut. Algoritma pembentukannya adalah sbb. :
1. Tetapkan : q0’ = q0 dan V T ’ = V T
2. Copykan tabel AHN F sebagai tabel AHD F’. Mula-mula Q’ = Q dan σ’ = σ
3. Setiap stata q yang merupakan nilai (atau peta) dari fungsi σ dan q ∉ Q, ditetapkan sebagai elemen baru dari Q’. Tempatkan q tersebut pada kolom Stata σ’, lakukan pemetaan berdasarkan fungsi σ.
4. Ulangi langkah (3) sampai tidak diperoleh stata baru.
5. Elemen Z’ adalah semua stata yang mengandung stata elemen Z.
Berikut ini diberikan sebuah contoh AHN F = (Q, V T , σ, q0, Z) dengan :2. Copykan tabel AHN F sebagai tabel AHD F’. Mula-mula Q’ = Q dan σ’ = σ
3. Setiap stata q yang merupakan nilai (atau peta) dari fungsi σ dan q ∉ Q, ditetapkan sebagai elemen baru dari Q’. Tempatkan q tersebut pada kolom Stata σ’, lakukan pemetaan berdasarkan fungsi σ.
4. Ulangi langkah (3) sampai tidak diperoleh stata baru.
5. Elemen Z’ adalah semua stata yang mengandung stata elemen Z.
Q = {A, B, C}, V T = {a, b}, q0 = A, Z = {C}, dan σ didefinisikan sebagai berikut:
Gambar5. Tabel AHN yang akan dikonversikan menjadi AHD
Jawab :
Berdasarkan algoritma di atas, maka :
1. q0’ = q0 = A, V T ’ = V T = {a, b}.
2. Hasil copy tabel AHN F menghasilkan tabel AHD F’ berikut :
Gambar6. Tabel AHD F’σ ([A,B],a) = σ (A,a) ∪ σ (B,a) = [A,B] ∪ A = [A,B], dan σ ([A,B],b) = σ (A,b) ∪ σ (B,b) = C ∪ B = [B,C], sehingga diperoleh tabel berikut :
Gambar7. Tabel AHD F’ yang sudah mempunyai satu stata baru
Gambar8. Tabel AHD F’ yang sudah jadi
5. Setelah langkah (4) di atas tidak terdapat lagi stata baru.
Dengan demikian AHD F’ yang dihasilkan adalah : AHD F’ = (Q’, V T ’, σ’, q0’,= Z’), dimana : Q’ = {A, B, C, [A,B], [B,C]}, V T ’ = {a, b}, q0’ = A, Z’ = {C, [B,C]}. Fungsi transisi σ’ serta graf dari AHD F’ adalah sebagai berikut :
Dengan demikian AHD F’ yang dihasilkan adalah : AHD F’ = (Q’, V T ’, σ’, q0’,= Z’), dimana : Q’ = {A, B, C, [A,B], [B,C]}, V T ’ = {a, b}, q0’ = A, Z’ = {C, [B,C]}. Fungsi transisi σ’ serta graf dari AHD F’ adalah sebagai berikut :
Gambar9. Tabel AHD F’ yang akan dijadikan graf danGrafik AHN Menjadi AHD
0 comments: